1、集合结构
1.1 概述
几乎每种编程语言中,都有集合结构
集合比较常见的是实现方式是哈希表
集合通常是一组无序的,不能重复的元素构成的。可以说集合是一个特殊的数组,特殊之处在集合里边的元素没有顺序, 也不能重复,这意味着不能通过下标值进行访问,相同的对象在集合中只会存在一份
学习方式:封装一个集合类(哈希表的实现方式后续补充)
1.2 集合结构的封装
代码解析
下列代码封装了一个集合的构造函数,在集合中,添加了一个items属性,用于保存之后添加到集合中的元素,因为Object的keys本身就是一个集合,后续我们给集合添加对应的操作方法
<script>
// 封装集合的构造函数
function Set (){
// 使用一个对象来保存集合的元素
this.items = {}
// 集合的操作方法
}
</script>
1.3 集合常见的结构
1、add(value):向集合添加一个新的项
2、remove(value):从集合中移除一个值
3、has(value):如果值在集合中(即意味着有重复值),返回true,否则返回false
4、clear():移除集合中的所有项
5、size():返回集合所包含的元素数量。与数组的length类似
6、values():返回一个包含集合所有值的数组
// 封装集合的构造函数
function Set (){
// 使用一个对象来保存集合的元素
this.items = {}
// 集合的操作方法
// add 方法
Set.prototype.add = function (value) {
// 检查集合中是否已经存在将要插入的值,已存在则返回false
if(this.has(value)){
return false
}
this.items[value] = value //向集合中添加key为value,值为value的一项
return true
}
// has 方法
Set.prototype.has = function (value) {
// hasOwnProperty() 方法用来检测一个属性是否是对象的自有属性,而不是从原型链继承的。如果该属性是自有属性,那么返回 true,否则返回 false。
// 换句话说,hasOwnProperty() 方法不会检测对象的原型链,只会检测当前对象本身,只有当前对象本身存在该属性时才返回 true
return this.items.hasOwnProperty(value)
}
// remove方法
Set.prototype.remove = function (value) {
// 判断集合中是否已包含该元素
if (!this.has(value)){
return false
}
delete this.items[value]
return true
}
//clear方法
Set.prototype.clear = function () {
this.items = {}
}
// size方法
Set.prototype.size = function () {
return Object.keys(this.items).length
}
// 获取集合中所有的值
Set.prototype.values = function () {
// Object.keys() 方法会返回一个由一个给定对象的自身可枚举属性组成的数组,数组中属性名的排列顺序和正常循环遍历该对象时返回的顺序一致 。
return Object.keys(this.items)
}
}
测试
// 测试
var game = new Set()
game.add("英雄联盟")
game.add("地下城与勇士")
game.add("原神")
game.add("QQ飞车")
alert(game.values())
alert(game.size())
game.remove("QQ飞车")
alert(game.values())
game.clear()
alert(game.values())
1.4 集合间操作
1、并集:对于给定的两个集合,返回一个包含两个集合中所有元素的新集合
2、交集:对于给定的两个集合,返回一个包含两个集合中共有元素的新集合
3、差集:对于给定的两个集合,返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合
4、子集:验证一个给定集合是否是另一个集合的子集
并集
代码解析
1、首先需要创建一个新的集合,代表两个集合的并集
2、遍历集合1中所有的值,并且添加到新集合中
3、遍历集合2中所有的值,添加到新集合中(这个过程中需要排除集合中出现重复的值)
4、将最终的新集合返回
// 集合间操作
// 并集
Set.prototype.union = function (otherSet) {
// this : 集合A
// otherSet : 集合B
// 1.创建新的集合
var unionSet = new Set()
// 2.将集合A中所有的元素添加进新集合中
var values = this.values()
for(var i = 0; i < values.length; i++){
unionSet.add(values[i])
}
//3.取出B集合中所有的元素添加进新集合中
values = otherSet.values()
for(var i = 0; i < values.length; i++){
unionSet.add(values[i]) //由于add函数已经做出判断,当新集合中已存在重复的元素,将不会将重复值添加进去
}
return unionSet
}
测试
// 测试集合间操作
var setA = new Set()
setA.add("数")
setA.add("据")
setA.add("结")
setA.add("构")
var setB = new Set()
setB.add("与")
setB.add("算法")
setB.add("算法") //会被排除
// 1.求两个集合的并集
unionSet = setA.union(setB)
alert(unionSet.values())
交集
// 交集
Set.prototype.intersection = function (otherSet) {
// 1.创建新的集合
var intersectionSet = new Set()
// 2.从A中取出一个个元素,判断是否同时存在于集合B中,存在放入新的集合中
var values = this.values()
for(var i = 0; i < values.length; i++){
var items = values[i]
if(otherSet.has(items)){
intersectionSet.add(items)
}
}
return intersectionSet
}
测试
// 2.求两个集合的交集
var aa = new Set()
aa.add(11)
aa.add(22)
aa.add(33)
var bb = new Set()
bb.add(22)
bb.add(33)
bb.add(44)
var res = aa.intersection(bb)
console.log(res.values());
差集
// 差集
Set.prototype.difference = function (otherSet) {
// 1.创建新的集合
var differenceSet = new Set()
// 从A中取出一个个元素,判断是否同时存在于集合B中,不存在则加入新的集合中
var values = this.values()
for(var i =0; i < values.length; i++){
var item = values[i]
if(!otherSet.has(item)) {
differenceSet.add(item)
}
}
return differenceSet
}
测试
var aa = new Set()
aa.add(11)
aa.add(22)
aa.add(33)
var bb = new Set()
bb.add(22)
bb.add(33)
bb.add(44)
// 3.求两个集合的差集
var res2 = aa.difference(bb)
console.log(res2.values()); //11
子集
判断集合A是否集合B的子集
// 判断A集合是否B集合的子集
Set.prototype.subset = function (otherSet) {
// 遍历集合A中所有的元素,如果发现,集合A中的元素,在集合B中不存在,那么false
// 如果遍历了整个集合,依然没有返回false,则返回true
var values = this.values()
for(var i = 0; i < values.length; i++){
var item = values[i]
if(!otherSet.has(item)){
return false
}
}
return true
}
2、字典结构
直接上代码
//创建字典的构造函数
function Dictionary() {
//字典的属性
this.items = {}
// 字典的操作方法
// 在字典中添加键值对
Dictionary.prototype.set = function (key,value) {
this.items[key] = value
}
// 判断字典中是否有某个key
Dictionary.prototype.has = function (key) {
return this.items.hasOwnProperty(key)
}
// 从字典中移除元素
Dictionary.prototype.remove = function (key) {
// 1. 判断字典中是否有这个key
if (!this.has(key)) return false
// 2.从字典中移除key
delete this.items[key]
return true
}
// 根据key去获取value
Dictionary.prototype.get = function (key) {
return this.has(key) ? this.items[key] : undefined
}
// 获取所有的keys
Dictionary.prototype.keys = function () {
return Object.keys (this.items)
}
// 获取所有的value
Dictionary.prototype.values = function () {
return Object.values(this.items)
}
// size方法
Dictionary.prototype.size = function () {
return this.keys().length
}
// clear方法
Dictionary.prototype.clear = function () {
this.items = {}
}
}
3、图结构
3.1 概述
在计算机程序设计中,图结构,也是一种非常常见的数据结构
什么是图?
1、图结构是一种与树结构有些相似的数据结构
2、图论是数学的一个分支,并且,在数学的概念上,树是图的一种
3、它以图为研究对象,研究顶点和边组成的图形的数学理论和方法
4、主要研究的目的是事物之间的关系,顶点代表事物,边代表两个事物间的关系
图结构的特点:
一组顶点:通常用V(Vertex)表示顶点的集合
一组边:通常用E(Edge)表示边的集合
注:边是顶点和顶点之间的连线、边可以是有向的,也可以是无向的。比如A---B,通常表示无向,A-->B通常表示有向
历史故事
18世纪著名古典数学问题的故事:
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛即岛与河岸连接起来。
有人提出问题:一个人怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点
著名数学家欧拉在解答问题的同时,开创了数学的一个新的分支——图论与几何拓扑
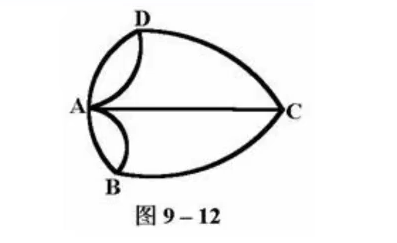
连接一点的边的数目如果是奇数条,就称为奇点,如果是偶数条就称为偶点。
要想一笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两端
因此任何图能一笔画成,奇点要么没有,要么在两端
图的相关术语
1、顶点
顶点表示图中的一个节点
2、边
表示顶点与顶点之间的连线
3、相邻顶点
由一条边连接在一起的顶点称为相连顶点
4、度
一个顶点的度是相邻顶点的数量
5、路径
简单路径:要求不包含重复的顶点
回路:第一个顶点和最后一个顶点相同的路径称为回路
6、无向图
所有的边都没有方向 如:A——B
7、有向图
表示图中的边是有方向的 如:A ——> B
8、无权图
边没有携带权重(不能说0-1的边,比4-9的边更远或者用的时间更长)
9、带权图
带权图表示边有一定的权重(这里的权重可以是任意希望表示的数据,比如顶点与顶点的距离)
图的表示方式
- 邻接矩阵
邻接矩阵让每一节点和一个整数相关联,该整数作为数组的下标
使用一个二维数组来表示顶点之间的连接
问题:如果图是一个稀疏图(顶点与顶点之间的关联很少),那么矩阵中存在大量的0,浪费了计算机的存储空间
- 邻接表
邻接表图中每个顶点以及和顶点相邻的顶点列表组成。这个列表有很多的方式来存储:数组/链表/哈希表
例如:如果要表示和A顶点有关联的顶点,A和B/C/D有边,那么我们可以通过A找到对应的数组,再取出其中的内容就可以了
问题:邻接表计算“出度”是比较简单的(出度:指向别人的数量,入度:指向自己的数量)
如果需要计算“入度”是麻烦的,必须构造一个“逆邻接表”。
3.2 封装图结构
function Graph () {
//属性
this.vertexes = [] //存储顶点
this.adjList = new Dictionary() // 存储边
// 方法
}
代码解析:
创建Graph的构造函数
vertexes :用于存储所有的顶点
adjList : adj是adjoin的缩写,邻接的意思。adjList 用于存储所有的边,这里采用邻接表的形式
3.3 图结构常用方法
1、添加顶点、边
function Graph () {
//属性
this.vertexes = [] //存储顶点
this.edges = new Dictionary() // 存储边(字典)
// 方法
// 1、添加顶点
Graph.prototype.addVertex = function (v) {
this.vertexes.push(v) //将顶点v添加到存储顶点的数组中
this.edges.set(v, []) // 创建以顶点v为键,[]为值的数组,用于存储边
}
// 2、添加边
Graph.prototype.addEdge = function (v1,v2) {
// 无向
this.edges.get(v1).push(v2) //根据顶点V1取出存储边的数组,将V2添加进去
this.edges.get(v2).push(v1) //同上
}
}
测试代码
// 测试代码
// 1.创建图结构
var graph = new Graph()
// 2.添加顶点
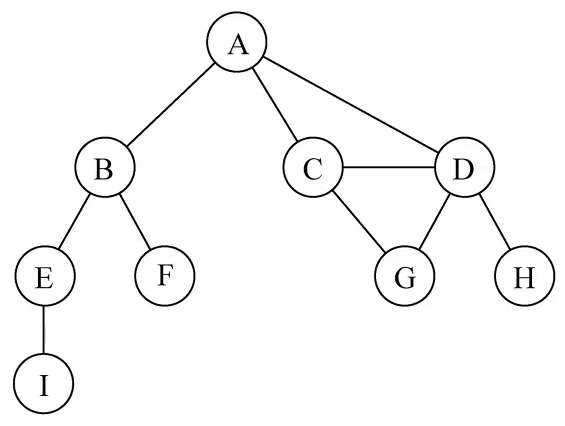
var myVertexes = ['A','B','C','D','E','F','G','H','I']
for(var i = 0; i < myVertexes.length; i++){
graph.addVertex(myVertexes[i])
}
// 3.添加边
graph.addEdge('A','B')
graph.addEdge('A','C')
graph.addEdge('A','D')
graph.addEdge('C','D')
graph.addEdge('C','G')
graph.addEdge('D','G')
graph.addEdge('D','H')
graph.addEdge('B','E')
graph.addEdge('B','F')
graph.addEdge('E','I')
添加完顶点与边,图结构如下:
2、toString方法
// 3、toString方法
Graph.prototype.toString = function () {
// 1.保存结果的字符串
var resultString = ""
// 2.遍历取出所有顶点
for(var i = 0; i < this.vertexes.length; i++){
resultString += this.vertexes[i] + "-->"
//3.取出对应顶点的边
var vEdges = this.edges.get(this.vertexes[i])
//4.遍历所有边
for(var j = 0; j < vEdges.length; j++){
resultString += vEdges[j] + " "
}
resultString += "\n"
}
// 将结果返回
return resultString
}
调用toString方法测试上边的图结构是否正确
// 调用toSTRING方法
console.log(graph.toString());
//输出:
A-->B C D
B-->A E F
C-->A D G
D-->A C G H
E-->B I
F-->B
G-->C D
H-->D
I-->E
图的遍历
1、图的遍历思想和树的遍历思想是一样的。
2、图的遍历意味着需要将图中每个顶点访问一遍,并且不能有重复的访问
两种算法可以对图进行遍历
广度优先搜索(Breadth-First Search,简称BFS)
基于队列,入队列的顶点先被探索
深度优先搜索(Depth-First Search,简称DFS)
基于栈或使用递归,通过将顶点存入栈中,顶点是沿着路径被探索的,存在新的相邻顶点就去访问
这两种遍历算法,都需要明确指定第一个被访问的顶点
为了记录顶点是否被访问过,可以使用三种颜色来反映它们的状态
1、白色:表示该顶点还没有被访问
2、灰色:表示该顶点被访问过,但并未被探索过
3、黑色:表示该顶点被访问过且被完全探索过
3、广度优先搜索
广度优先算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访问图的一层。换句话说,就是先宽后深的访问顶点。(不解)
// 初始化状态颜色
Graph.prototype.initializeColor = function () {
var colors = []
for (var i = 0; i < this.vertexes.length; i++){
colors[this.vertexes[i]] = 'white'
}
return colors
}
// 实现广度优先搜索
Graph.prototype.bfs = function (initV,handler) {
// 1.初始化颜色
var colors = this.initializeColor()
// 2.创建队列
var queue = new Queue()
// 3.将顶点加入到队列中
queue.enqueue(initV)
// 4.循环从队列中取出元素
while (!queue.isEmpty()) {
// 4.1从对列中取出一个顶点
var v = queue.dequeue()
// 4.2获取和顶点相连的另外顶点
var vList = this.edges.get(v)
// 4.3将v的颜色设置成灰色
colors[v] = 'gray'
// 4.4遍历所有的顶点,并且加入到队列中
for (var i = 0; i < vList.length; i++) {
var e = vList[i]
if (colors[e] == 'white') {
colors[e] = 'gray'
queue.enqueue(e)
}
}
// 4.5访问顶点
handler(v)
// 4.6将顶点设置成黑色
colors[v] = 'black'
}
}
测试代码
// 测试bfs
var result = ''
graph.bfs(graph.vertexes[0],function(v){
result += v + ' '
})
alert(result)
//输出:A B C D E F G H I
4、深度优先搜索
思路:
深度优先搜索算法将会从第一个指定的顶点开始遍历图,沿着路径知道这条路径最后被访问了
接着原路回退并探索下一条路径
// 深度优先搜索(DFS)
Graph.prototype.dfs = function (initV,handler) {
// 1.初始化颜色
var colors = this.initializeColor()
// 2.从某个顶点开始一次递归访问
this.dfsVisit(initV,colors,handler)
}
// dfs的递归函数
Graph.prototype.dfsVisit = function (v,colors,handler) {
// 1.将颜色设置为灰色
colors[v] = 'gray'
// 2.处理v顶点
handler(v)
// 3.访问v相连的顶点
var vList = this.edges.get(v)
for (var i = 0; i < vList.length; i++) {
var e = vList[i]
if (colors[e] == 'white') {
this.dfsVisit(e,colors,handler)
}
}
// 4.将v设置成为黑色
colors[v] = 'black'
}
测试代码
// 测试dfs
result = ''
graph.dfs(graph.vertexes[0],function(v){
result += v + ' '
})
alert(result)
//输出:A B E I F C D G H
4、排序算法
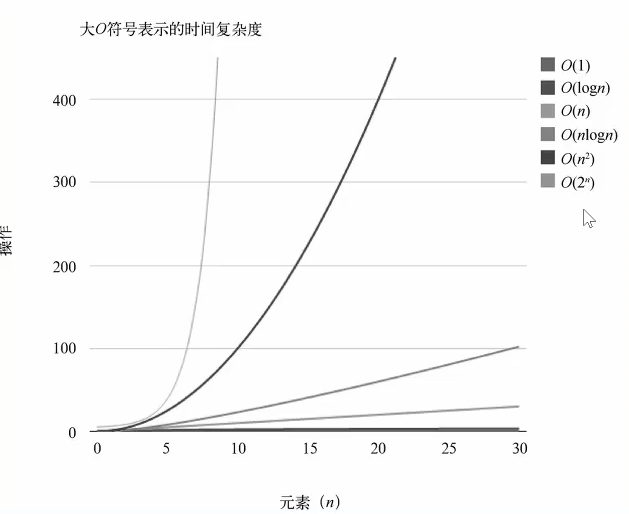
4.1 大O表示法
理解
公司可以按照规模分为:小型企业、中型企业、大型企业。(在不说明具体员工人数和占地面积的情况下,通过这样子大概的概念来描述企业的规模)
在算法的描述中,我们也可以通过类似的快捷方式来描述计算机算法的效率,这种粗略的度量被称为“ 大O ”表示法
大0表示法
如何比较哪个算法更好?
有人会说:算法A比算法B快两倍,但是这样的比较有时候没有意义
因为在数据项个数发生变化时,算法的效率会跟着发生改变,所以我们通常使用一种:算法的速度如何跟随数据量的变化的
| 符号 | 名称 |
|---|---|
| O(1) | 常数的 |
| O(log(n)) | 对数的 |
| O(n) | 线性的 |
| O(nlog(n)) | 线性和对数乘积 |
| O(n²) | 平方 |
| O(2ⁿ) | 指数的 |
推导大0表示法
1、用常量1取代运行时间中所有的加法常量
2、在修改后的运行次数函数中,只保留最高阶项
3、如果最好存在且不为1,则去除与这个项目相乘的常数
4.2 认识排序算法
排序算法有很多:冒泡排序、选择排序、插入排序、归并排序、基数排序、计数排序、希尔排序、堆排序、桶排序
什么时候用到排序算法?
当我们将数据放置在某个数据结构中存储起来后(比如数组),就很可能根据需求对数据进行不同方式的排序
排序算法的实现
// 创建列表类
function ArrayList () {
// 属性
this.array = []
// 方法
// 将数据插入数组
ArrayList.prototype.insert = function (item) {
this.array.push(item)
}
// toString
ArrayList.prototype.toString = function () {
return this.array.join('-')
}
// 实现排序的算法
// 冒泡排序
// 选择排序
// 插入排序
// 希尔排序
// 快速排序
}
// 测试类
var list = new ArrayList()
// 插入元素
list.insert(66)
list.insert(88)
list.insert(12)
list.insert(87)
list.insert(100)
list.insert(5)
list.insert(566)
list.insert(23)
alert(list)
实现两个元素位置的交换
由于在排序算法中经常用到该功能,所以可以进行统一封装
// 交换两个位置的数据
ArrayList.prototype.swap = function (m,n) {
var temp = this.array[m] //保存this.array(m)的状态
this.array[m] = this.array[n]
this.array[n] = temp
}
4.3 冒泡排序
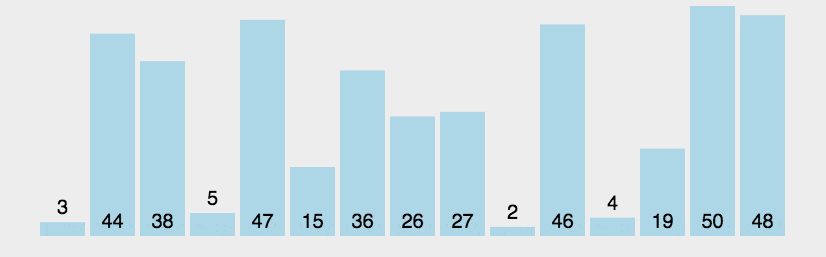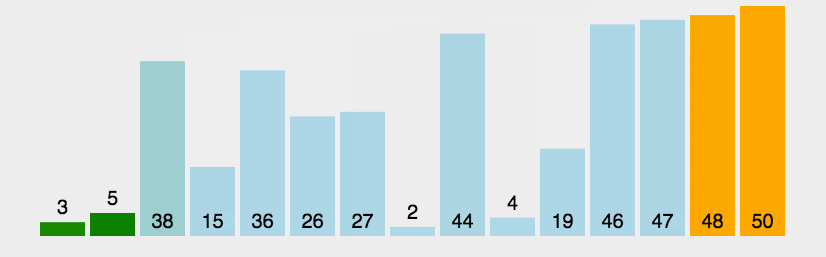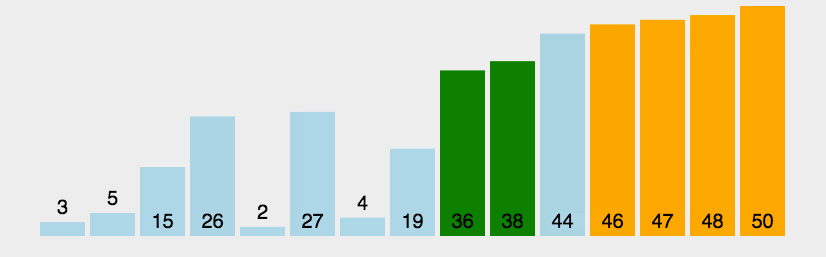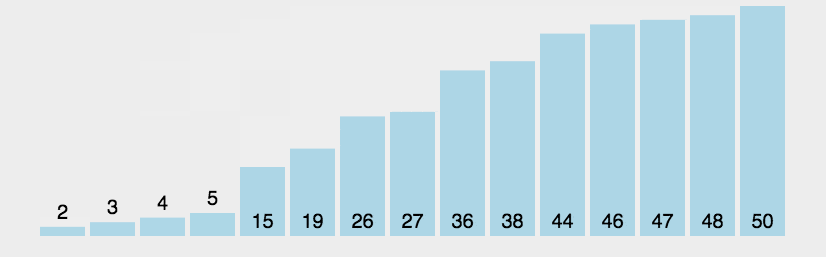
冒泡排序算法相对于其他排序运行效率较低,但是在概念上它是排序算法中最简单的
冒泡排序的思路:
1、对未排序的各元素从头到尾依次比较相邻的两个元素大小关系
2、如果左边的元素大于右边,则两者交换位置
3、大的元素向右再进行比较,依次类推,当走到最右端时,最高的元素一定就被放在了最右边
4、按照这个思路,从最左端重新开始,这次走到倒数第二个位置即可
5、依次类推,最终实现了升序排序
假设:有一个长度为10的数组里边,装满了各不相同的数值,要求从小到大排序
// 冒泡排序
ArrayList.prototype.bubblesort = function () {
// 1.获取数组的长度
var length = this.array.length
// 第一次:j = length-1,比较到倒数第一个位置
// 第二次:j = length-2,比较到倒数第二个位置
// 。。。
for (var i = length -1; i >= 0; i--) { //保证每次对比会跟前一次减少一位
// 第一次进来:i=0,比较0和1位置的两个数据
// 最后一次进来:i = length -2,比较length-2和length-1的两个数据
for(var j = 0; j < i; j++) {
if(this.array[j] > this.array[j+1]){
// 交换位置
this.swap(j,j+1)
}
}
}
}
理解
冒泡排序的效率
对于上图来说,一共有7个数字,每次循环进行了几次的比较呢?
第一次循环6次比较,第二次5次比较,第三次4次比较....直到最后一趟进行了一次比较。
所以,对于7个数据比较次数:6+5+4+3+2+1
对于N个数据项来说几次比较呢?(N-1) + (N-2) + (N-3) +...+1 = N * (N-1) / 2
推算大O表示法
1、N * (N-1) / 2 = N² / 2 - N /2 ,根据规则2:只保留最高项,变成 N² / 2
2、N² / 2,根据规则3,去除最高项的常量,变成N²
3、因此冒泡排序的比较次数的大O表示法为O(N² )
测试代码
// 测试类
var list = new ArrayList()
// 插入元素
list.insert(66)
list.insert(88)
list.insert(12)
list.insert(87)
list.insert(100)
list.insert(5)
list.insert(566)
list.insert(23)
alert(list)
// 测试冒泡排序
list.bubblesort()
alert(list)
4.4 选择排序
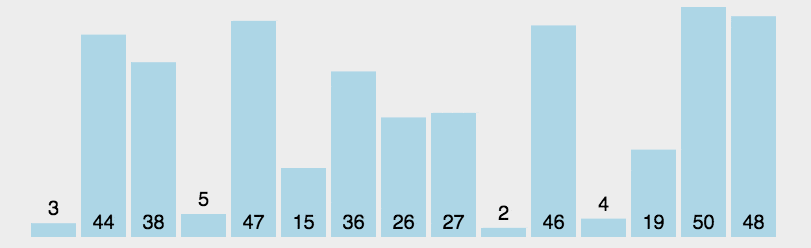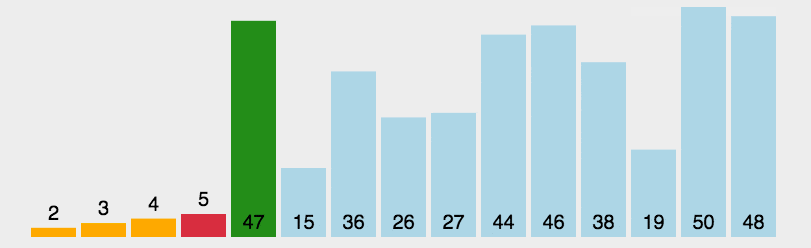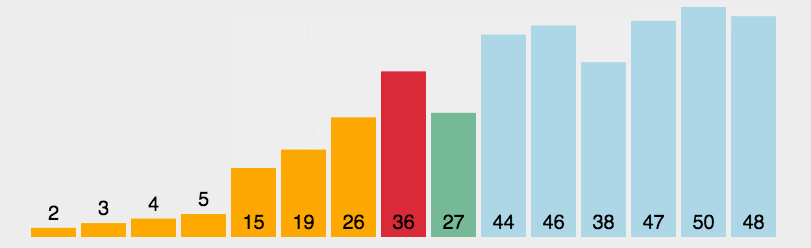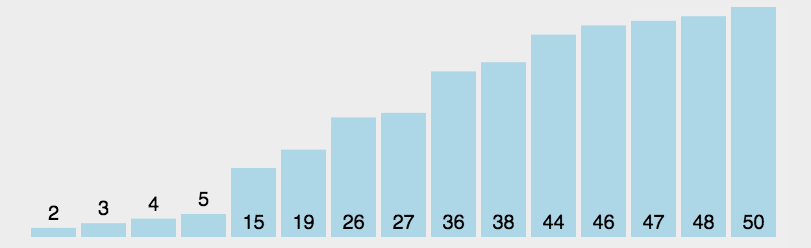
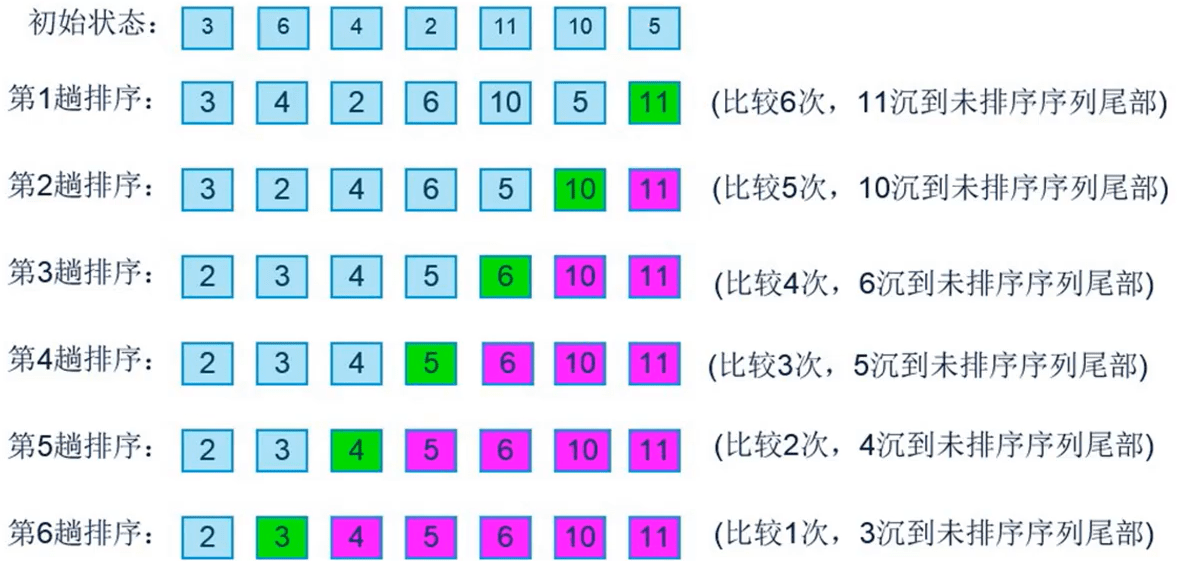
选择排序改进了冒泡排序: 将交换的次数由O(N²)减少到了O(N),但是比较的次数依然是O(N²)
思路
1、选定第一个索引位置,然后和后面元素一次比较。
2、如果后面的元素小于第一个索引位置的元素,则交换位置
3、经过第一轮比较后,可以确定第一个位置是最小的
4、然后使用同样的方法把剩下的元素逐个比较即可
5、可以看出选择排序,第一轮会选出最小值,第二轮会选出第二小的值,直到最后。
// 选择排序
ArrayList.prototype.selectionSort = function () {
// 1.获取数组的长度
var length =this.array.length
// 2.外层循环:依次从数组中取出元素。
// (最后一个值不用,因为最后的值,没人能跟它比较,它是最大值,所以j < length -1)
for (j = 0; j < length - 1; j++) {
// 3.内层循环
var min = j
for(var i = min + 1; i < length; i++) {
if (this.array[min] > this.array[i]) {
min = i //说明min不是最小值了,交换索引位置
}
}
// 遍历完成后,min记录了最小值的位置
this.swap(min,j)
}
}
测试代码
// 测试交换排序
list.selectionSort()
alert(list)
4.5 插入排序
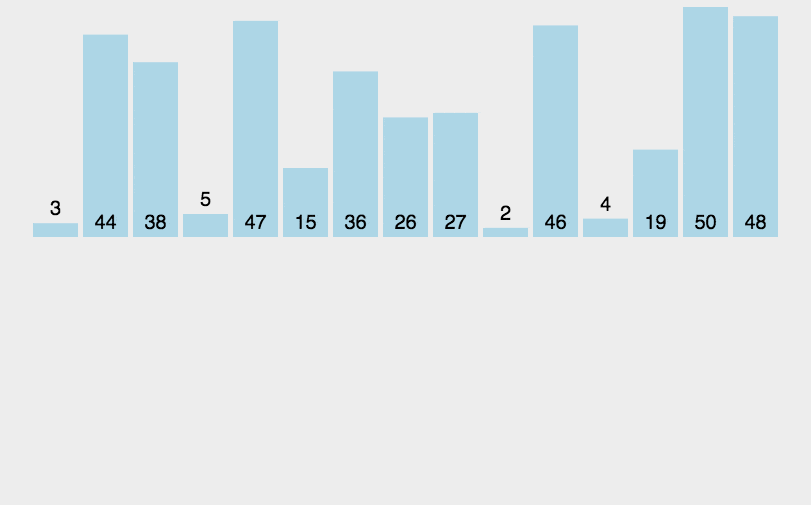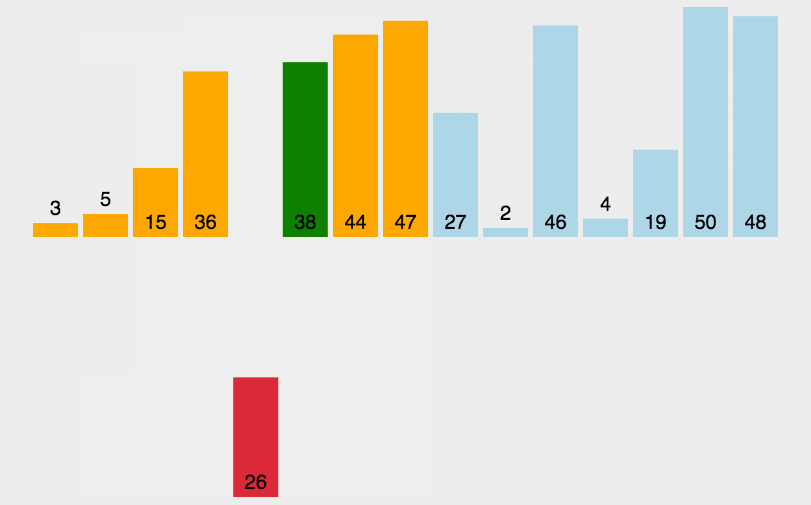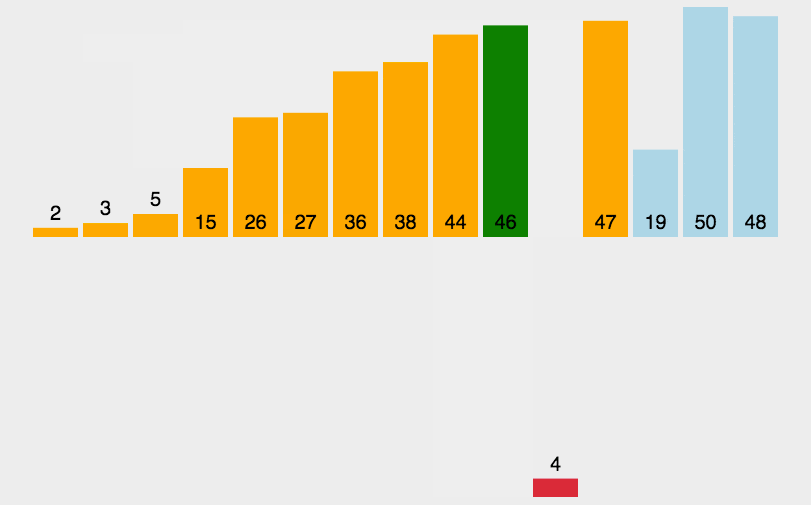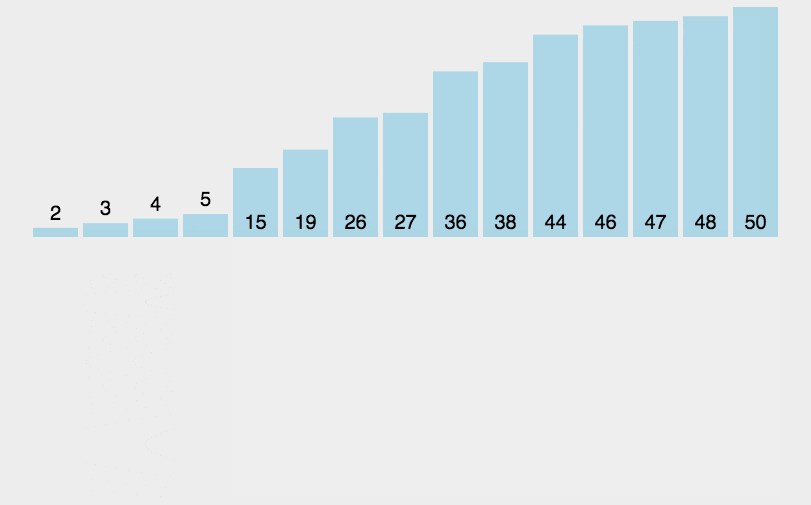
插入排序是简单排序中效率最好的一种,插入排序也是学习其他高级排序的基础
局部有序:
1、插入排序思想的核心是局部有序。比如在一个队列中的人,我们选择其中一个作为标记,这个被标记的人的左右队员已经是局部有序的。这意味着有一部分人是按顺序排列好的,有一部分还没有顺序
插入排序的思路
1、从第一个元素开始,该元素可以认为已经被排序
2、取出下一个元素,在已经排序的元素序列中从后向前扫描
3、如果该元素(已排序)大于新元素,将该元素移到下一个位置
4、重复上一个步骤,直到找到已排序的元素小于或者等于新元素的位置
5、将新元素插入到该位置后,重复上边的步骤
// 插入排序
ArrayList.prototype.insertionSort = function () {
// 获取数组的长度
var length =this.array.length
// 外层循环
for (var i = 1; i < length; i++) {
var temp = this.array[i] //记录现在循环到的值
var j = i //记录现在的索引
while (this.array[j - 1] > temp && j > 0) { //上一个值大于现在的值,说明要交换位置
this.array[j] = this.array[j - 1]
j--
}
// 不进入循环,说明不用交换位置了
this.array[j] = temp
}
}
4.6 希尔排序
希尔排序是插入排序的一种高效的改进版,并且效率比插入排序还要更快。
希尔排序的历史背景:
1、简单排序出现后的很长一段时间内,人们发明了各种各样的算法,但最终发现算法的时间复杂度都是O(N²),似乎没办法超越
2、计算机学术界充斥着“排序算法不可突破O(N²)”的声音
3、直到1959年,一位名为希尔的科学家发现了超越O(N²)的新排序算法。
希尔排序的思路
假如存在如下一组数据,我们可以先采用间隔为5进行分组,再对组内进行排序。采用间隔为3进行分组,排序。
最后是采用间隔为1进行分组排序,最终实现了较高效率的希尔排序
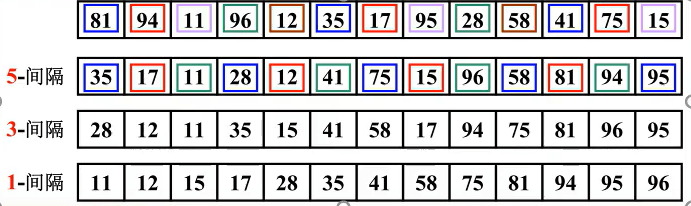
选择合适的增量(间隔gap)
1、在希尔排序的原稿中,建议测初始间距是N / 2 ,简单的把每趟排序分成两半
2、对于N = 100的数组来说,增量的序列为50、25、12、6、3、1
封装实现
// 希尔排序
ArrayList.prototype.shellSort = function () {
//1. 获取数组的长度
var length = this.array.length
//2. 初始化的增量(gap -> 间隔)
var gap = Math.floor(length / 2)
// 3.while循环(gap不断地减小)
while (gap >= 1) {
// 4.以gap作为间隔,进行分组,对分组进行插入排序
for (var i = gap; i < length; i++) {
var temp =this.array[i]
var j = i
while (this.array[j - gap] > temp && j > gap - 1) {
this.array[j] =this.array[j - gap]
j -= gap
}
// 5.将j位置的元素赋值temp
this.array[j] = temp
}
gap = Math.floor(gap / 2)
}
}
// 测试希尔排序
list.shellSort()
alert(list)
希尔排序的效率
希尔排序的效率跟增量是有关系的,但是证明它的效率非常困难,甚至某些增量的效率到目前依然没有被证明出来。
但是经过统计,希尔排序使用原始增量,最坏的情况下时间复杂度为O(N²),通常情况下都要好于O(N²)
4.7 快速排序
快速排序是目前所有排序算法中,最快的一种算法,被列为20世纪十大算法之一
希尔排序相当于插入排序的升级版,快速排序则是冒泡排序的升级版。
快速排序最重要的思想是分而治之。
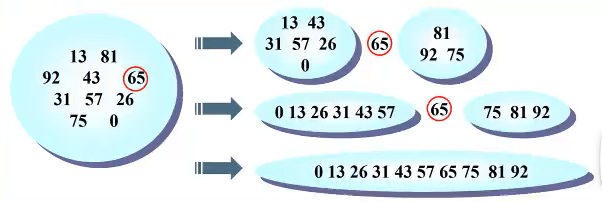
实现步骤
1、假设第一步从其中选出了65,通过算法将所有小于65的数字放在65的左边,大于65的数字放在65的右边。
2、分别将65左边、右边的数字看成整体,从中再分别取出一个数字,重复以上操作
快速排序的枢纽
1、在快速排序中有一个很重要的步骤就是选取枢纽(主元)
比较好的方式就是选取数据的头,中,尾。比较三者的大小,取处于中间的值
//具体代码
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
let left = [];
let right = [];
let midPoint = Math.floor(arr.length / 2)
const middle = arr.splice(midPoint,1)[0]
for (let i = 0; i < arr.length; i++) {
arr[i] < middle?left.push(arr[i]) : right.push(arr[i]);
}
return [...quickSort(left),middle,...quickSort(right)]
}

